It is possible to specify the method of interpolation to be used for non-linear function
tables by use of the interpolation attribute of the <independentVarPts> and <independentVarRef>
elements. This attribute, combined with the 'extrapolate' flag, provide several different
ways of realizing the intermediate values of the function when not at one of the specified
intersections of independent values.
Implementation of the specific interpolation algorithm is left up to the application, however, the following implementation notes are suggested:
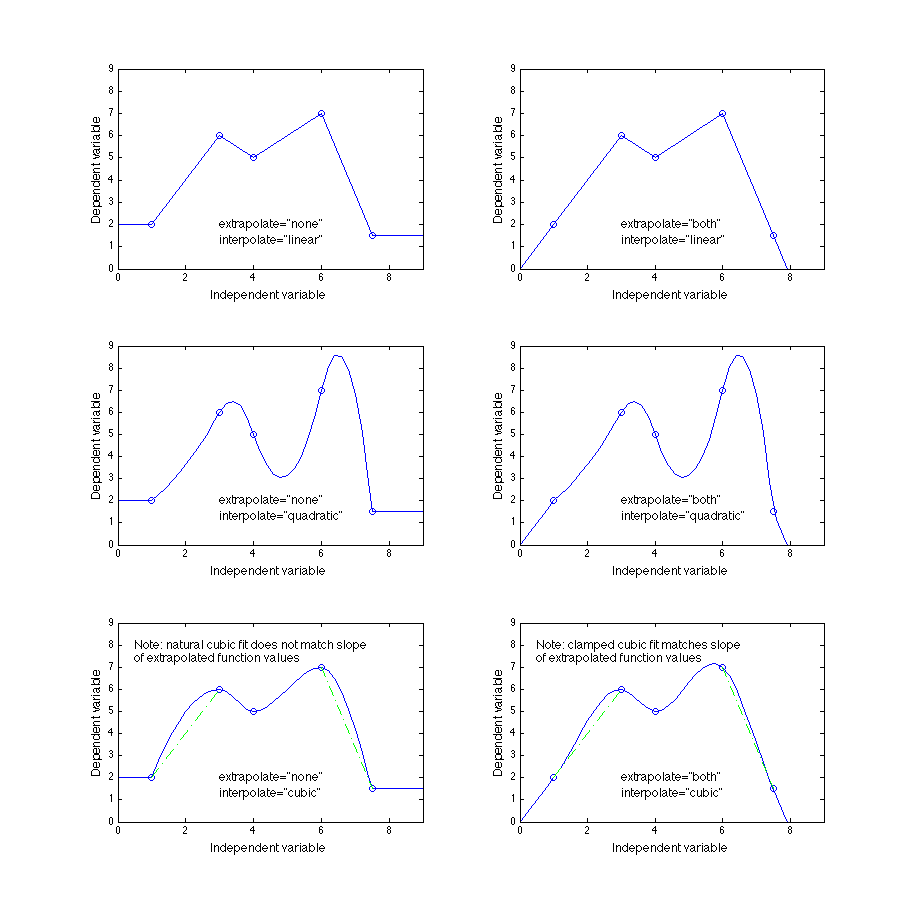
An infinite set of quadratic interpolations are possible; it is suggested to use the one that minimizes either the deviation from a linear interpolation or the slope error at any edge.
For cubic interpolation, the natural cubic spline (which has a second derivative of zero at each end) implementation is suggested when the 'extrapolate' attribute is 'none'. When the 'extrapolate' attribute is 'both', a clamped cubic spline that matches the extrapolation slopes is suggested.
For the discrete interpolation values (discrete, ceiling, or floor) the value of the 'extrapolate' attribute is meaningless.
The figures below give nine different examples for a one-dimensional table whose independent values are [1, 3, 4, 6, 7.5] with dependent values of [2, 6, 5, 7, 1.5].
Figure 4.
Example of the three discrete enumeration values of interpolate
attribute of the <independentVarPts> and <independentVarRef> elements for a
one-dimensional function table.
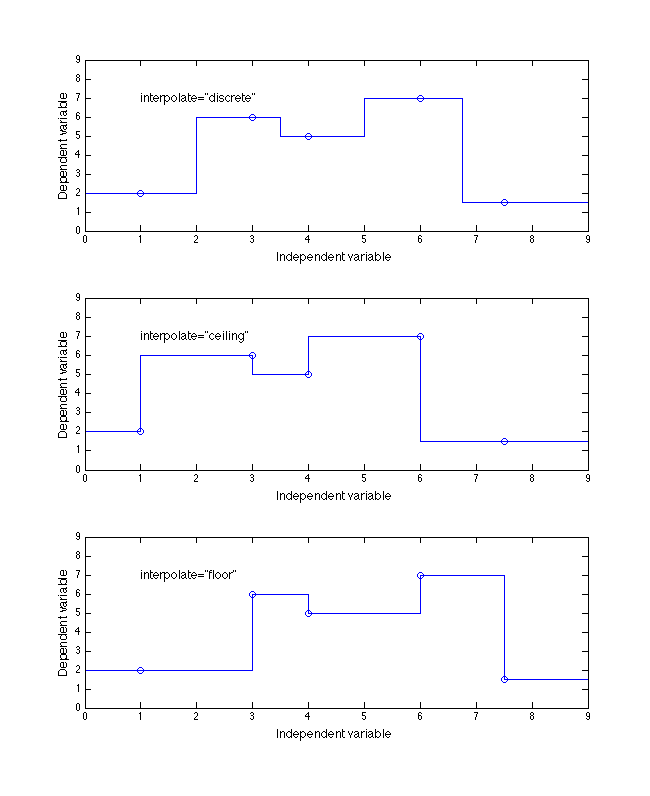
Figure 5.
Examples of the three higher-order interpolation methods showing the effect of the
interpolate attribute of the
<independentVarPts> and
<independentVarRef> elements for a one-dimensional function
table.