The ungriddedTableDef
element defines a set of non-orthogonal data points, along with their independent values
(coordinates), corresponding with the dependent value of an arbitrary function.
A 'non-orthogonal' data set, as opposed to a gridded or 'orthogonal' data set, means that the independent values are not laid out in an orthogonal grid. This form must be used if the dependent coordinates in any table dimension cannot be expressed by a single monotonically-increasing vector.
See the examples below for two instances of ungridded data.
An optional uncertainty element
may be provided that represents the statistical variation in the values presented. See
the section on Statistics below for more information
about this element.
ungriddedTableDef* : [utID, name, units]
description? :
(description character data)
provenance? :
author : name, org, [email]
address? :
(address character data)
functionCreationDate :
(date in YYYY-MM-DD format, character data)
documentRef* : docID
modificationRef* : modID
uncertainty? : effect
(normalPDF : numSigmas | uniformPDF : symmetry )
dataPoint+ :
ungriddedTableDef
attributes:
utIDA mandatory XML-legal name that is unique within the file
nameAn optional UNICODE name for the table (may be same as
gtID.unitsOptional units-of-measure for the table's output signal.
ungriddedTableDef
sub-elements:
descriptionThe optional description element allows the author to describe the data contained within this
ungriddedTable.provenanceThe optional provenance element allows the author to describe the source and history of the data within this
ungriddedTable.uncertaintyThis optional element, if present, describes the uncertainty of this parameter. See the section on Statistics below for more information about this element.
dataPointOne or more sets of coordinate and output numeric values of the function at various locations within it's input space. This element includes one coordinate for each function input variable. Parsing this information into a usable interpolative function is up to the implementor. By convention, the coordinates are listed in the same order that they appear in the using function.
Example 9.
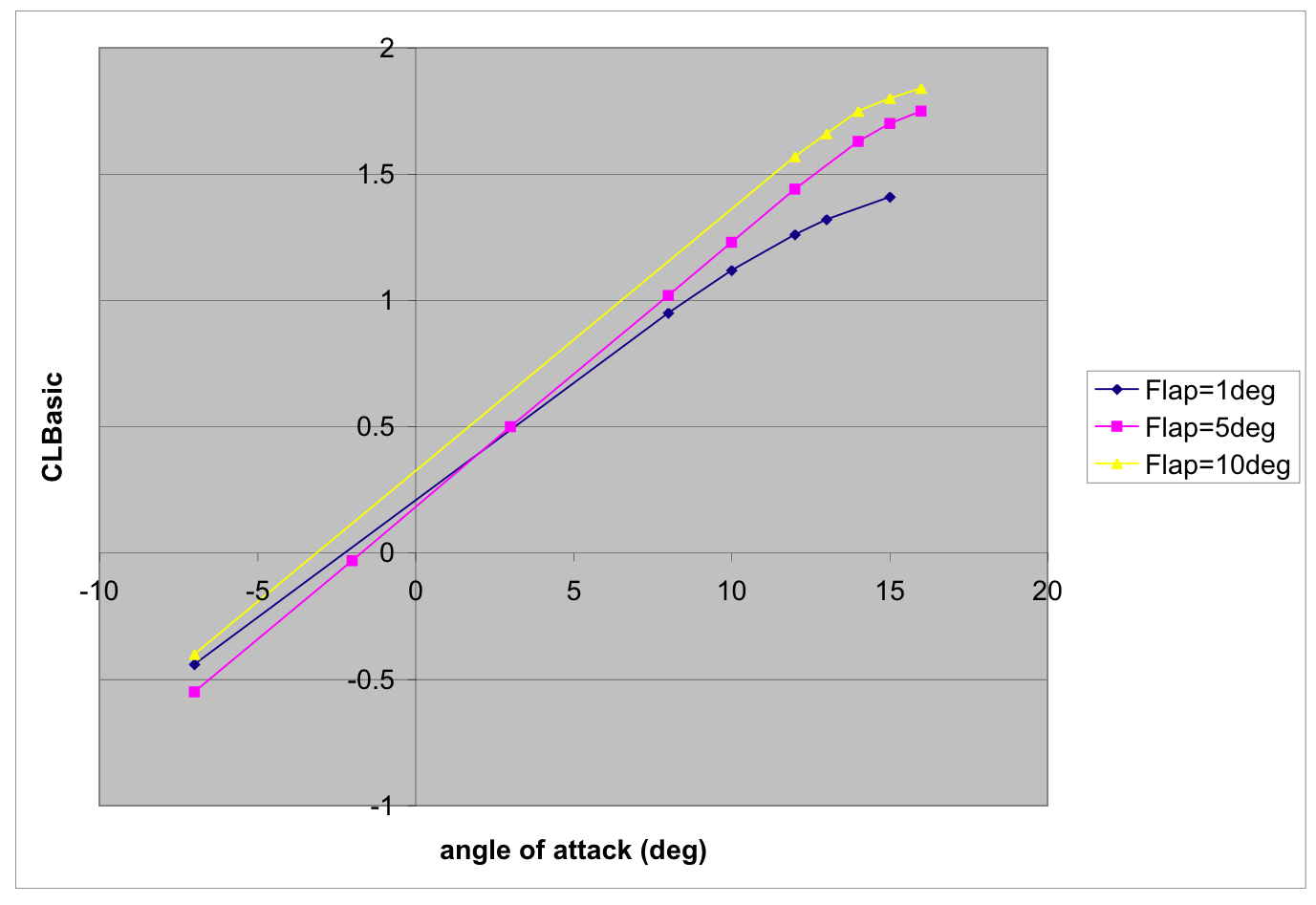
An example of an ungriddedTableDef element, encoding the data shown
in figure 2.
This two-dimensional function table is an example provided by Dr. Peter Grant of the
University of Toronto. Such a table definition would be used in a subsequent
function to describe how an output variable would be defined based
on two independent input variables. The function table doesn't indicate which input
and output variables are represented; this information is supplied by the
function element later so that a single function table can be
reused by multiple functions.
Note that in this example, the Mach breakpoints are orthogonally spaced while the angle of attack breakpoints are not; this is still an 'ungridded' table since at least one independent variable has non-orthogonal spacing.
<ungriddedTableDef name="CLBASIC as function of flap angle and angle of
attack" utID="CLBAlfaFlap_Table" units="ND">
<description>
CL basic as a function of flap angle and angle of attack. Note the alpha
used in this table is with respect to the wing design plane (in degrees).
Flap is in degrees as well.
</description>
<provenance>
<author name="Peter Grant" org="UTIAS"/> 
<functionCreationDate date="2006-11-01"/>
<documentRef refID="PRG1" />
</provenance>
<!--For ungridded tables you provide a list of dataPoints--> 
<dataPoint> 1.0 -5.00 -0.44 <!-- alfawdp, flap, CLB--></dataPoint> 
<dataPoint> 1.0 10.00 0.95 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 1.0 12.00 1.12 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 1.0 14.00 1.26 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 1.0 15.00 1.32 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 1.0 17.00 1.41 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 -5.00 -0.55 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 0.00 -0.03 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 5.00 0.50 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 10.00 1.02 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 12.00 1.23 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 14.00 1.44 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 16.00 1.63 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 17.00 1.70 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 5.0 18.00 1.75 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 10.0 -5.00 -0.40 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 10.0 14.00 1.57 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 10.0 15.00 1.66 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 10.0 16.00 1.75 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 10.0 17.00 1.80 <!-- alfawdp, flap, CLB--></dataPoint>
<dataPoint> 10.0 18.00 1.84 <!-- alfawdp, flap, CLB--></dataPoint>
</ungriddedTableDef>
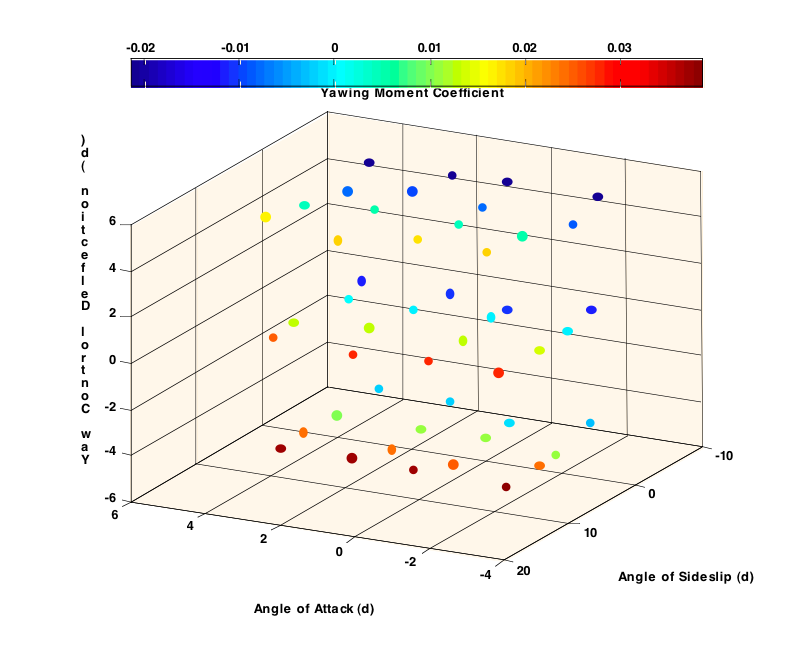
Example 10.
An excerpt from a sample aero model giving an example of a three-dimensional
ungriddedTableDef element, encoding the data shown in figure 3.
In this example, the dependent coordinates all vary in each dimension.
<!--===================================-->
<!-- Three-D Table Definition Example -->
<!--===================================-->
<ungriddedTableDef name="yawMomentCoefficientTable1" units="ND" utID="yawMomentCoefficientTable1">
<dataPoint> -1.8330592 -5.3490387 -4.7258599 -0.00350641</dataPoint>
<dataPoint> -1.9302179 -4.9698462 0.2798654 -0.0120538</dataPoint>
<dataPoint> -2.1213095 -5.0383145 5.2146443 -0.0207089</dataPoint>
<dataPoint> 0.2522004 -4.9587161 -5.2312860 -0.000882368</dataPoint>
<dataPoint> 0.3368831 -5.0797159 -0.3370540 -0.0111846</dataPoint>
<dataPoint> 0.2987289 -4.9691198 5.2868938 -0.0208758</dataPoint>
<dataPoint> 1.8858257 -5.2077654 -4.7313074 -0.00219842</dataPoint>
<dataPoint> 1.8031083 -4.7072954 0.0541231 -0.0111726</dataPoint>
<dataPoint> 1.7773659 -5.0317988 5.1507477 -0.0208074</dataPoint>
<dataPoint> 3.8104785 -5.2982162 -4.7152852 -0.00225906</dataPoint>
<dataPoint> 4.2631596 -5.1695257 -0.1343410 -0.0116563</dataPoint>
<dataPoint> 4.0470946 -5.2541017 5.0686926 -0.0215506</dataPoint>
<dataPoint> -1.8882611 0.2422452 -5.1959304 0.0113462</dataPoint>
<dataPoint> -2.1796091 0.0542085 0.2454711 -0.000253915</dataPoint>
<dataPoint> -2.2699103 -0.3146657 4.8638859 -0.00875431</dataPoint>
<dataPoint> 0.0148579 0.1095599 -4.9639500 0.0105144</dataPoint>
<dataPoint> -0.1214591 -0.0047960 0.2788827 -0.000487753</dataPoint>
<dataPoint> 0.0610233 0.2029588 5.0831767 -0.00816086</dataPoint>
<dataPoint> 1.7593356 -0.0149007 -5.0494446 0.0106762</dataPoint>
<dataPoint> 1.9717048 -0.0870861 0.0763833 -0.000332616</dataPoint>
<dataPoint> 2.0228263 -0.2962294 5.1777078 -0.0093807</dataPoint>
<dataPoint> 4.0567507 -0.2948622 -5.1002243 0.010196</dataPoint>
<dataPoint> 3.6534822 0.2163747 0.1369900 0.000312733</dataPoint>
<dataPoint> 3.6848003 0.0884533 4.8214805 -0.00809437</dataPoint>
<dataPoint> -2.3347682 5.2288720 -4.7193014 0.02453</dataPoint>
<dataPoint> -2.3060350 4.9652745 0.2324610 0.0133447</dataPoint>
<dataPoint> -1.8675176 5.0754646 5.1169942 0.00556052</dataPoint>
<dataPoint> 0.0004379 5.1220145 -5.2734993 0.0250468</dataPoint>
<dataPoint> -0.1977035 4.7462188 0.0664495 0.0124083</dataPoint>
<dataPoint> -0.1467742 5.0470092 5.1806131 0.00475277</dataPoint>
<dataPoint> 1.6599338 4.9352809 -5.1210532 0.0242646</dataPoint>
<dataPoint> 2.2719825 4.8865093 0.0315210 0.0125658</dataPoint>
<dataPoint> 2.0406858 5.3253471 5.2880688 0.00491779</dataPoint>
<dataPoint> 4.0179983 5.0826426 -4.9597629 0.0243518</dataPoint>
<dataPoint> 4.2863811 4.8806558 -0.2877697 0.0128886</dataPoint>
<dataPoint> 3.9289361 5.2246849 4.9758705 0.00471241</dataPoint>
<dataPoint> -2.2809763 9.9844584 -4.8800790 0.0386951</dataPoint>
<dataPoint> -2.0733070 9.9204337 0.0241722 0.027546</dataPoint>
<dataPoint> -1.7624546 9.9153493 5.1985794 0.0188357</dataPoint>
<dataPoint> 0.2279962 9.8962508 -4.7811258 0.0375762</dataPoint>
<dataPoint> -0.2800363 10.3004593 0.1413907 0.028144</dataPoint>
<dataPoint> 0.0828562 9.9008011 5.2962722 0.0179398</dataPoint>
<dataPoint> 1.8262230 10.0939436 -4.6710211 0.037712</dataPoint>
<dataPoint> 1.7762123 10.1556398 -0.1307093 0.0278079</dataPoint>
<dataPoint> 2.2258599 9.8009720 4.6721747 0.018244</dataPoint>
<dataPoint> 3.7892651 9.8017197 -4.8026383 0.0368199</dataPoint>
<dataPoint> 4.0150716 9.6815531 -0.0630955 0.0252014</dataPoint>
<dataPoint> 4.1677953 9.8754433 5.1776223 0.0164312</dataPoint>
</ungriddedTableDef>
