It is possible to specify the method of interpolation to be used for nonlinear
function tables by use of the interpolate attribute of the
independentVarPts and
independentVarRef elements. This attribute, combined with the
extrapolate flag, provides several different ways of realizing the
intermediate values of the function when not at one of the specified intersections of
independent values.
Possible values for the interpolate attribute are:
-
discrete Output uses value associated with nearest breakpoint
-
floor Output uses value associated with next (numerically higher) breakpoint
-
ceiling Output uses value associated with last (numerically lower) breakpoint
-
linear(default) Output is linearly interpolated between breakpoints
-
quadraticSpline Output follows a quadratic spline fit through values associated with two nearby breakpoints
-
cubicSpline Output follows a cubic spline fit through values associated with three nearby breakpoints
Possible values for the extrapolate attribute are:
-
neither(default) Output is held constant at value associated with closest end of breakpoints if the input value is outside the limits of the associated breakpoint set
-
min Output follows extrapolated values of function if the input is below the minimum breakpoint value
-
max Output follows extrapolated values of function if the input is above maximum breakpoint value
-
both Output follows extrapolated values of function if the input is outside the limits of the associated breakpoint set
Implementation of the specific interpolation algorithm is left up to the implementer. One reference is the Wikipedia entry on interpolation [wiki01].
The following implementation notes are suggested:
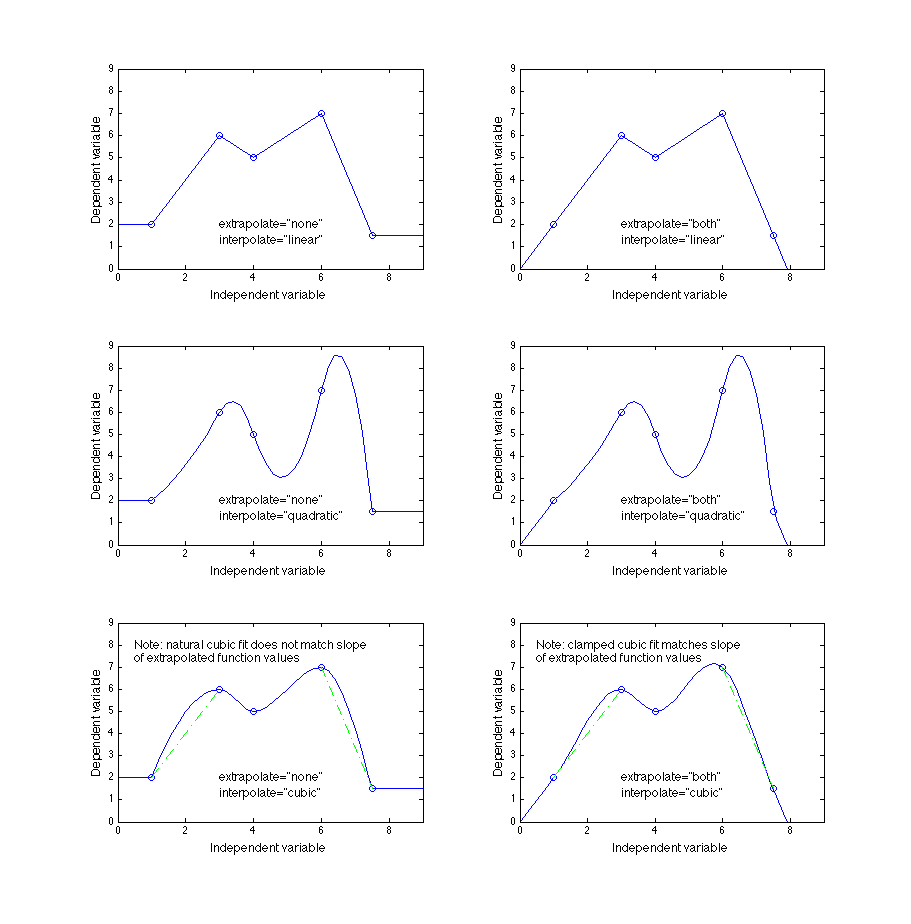
An infinite set of quadratic interpolations are possible; it is suggested to use the one that minimizes either the deviation from a linear interpolation or the slope error at any edge.
For cubic interpolation, the natural cubic spline (which has a second derivative of zero at each end) is recommended when the
extrapolateattribute isnone. When theextrapolateattribute isboth, a clamped cubic spline that matches the extrapolated slope of the last two data points is suggested.For the discrete interpolation values (
discrete,ceiling, orfloor), the value of theextrapolateattribute is meaningless.
For discrete interpolation,
discreteimplies the change between output values occurs midway between independent breakpoint values, as shown in the top plot of Figure 4.ceilingmeans the output takes on the value of the next-higher dependent variable breakpoint as soon as each independent breakpoint value is passed (assuming the input value is increasing) as shown in the middle plot of Figure 4.floormeans the output retains the value of the last dependent variable breakpoint until the next independent breakpoint value is reached (assuming the input value is increasing) as shown in the bottom plot of Figure 4.
The default value for interpolate is linear. The
default value for extrapolate is neither.
Figures 4 and 5 below give nine different examples for a 1D table whose independent values are [1, 3, 4, 6, 7.5] with dependent values of [2, 6, 5, 7, 1.5].
Figure 4. Example of the three discrete enumeration values of interpolate
attribute of the independentVarPts and
independentVarRef elements for a 1D
function table.
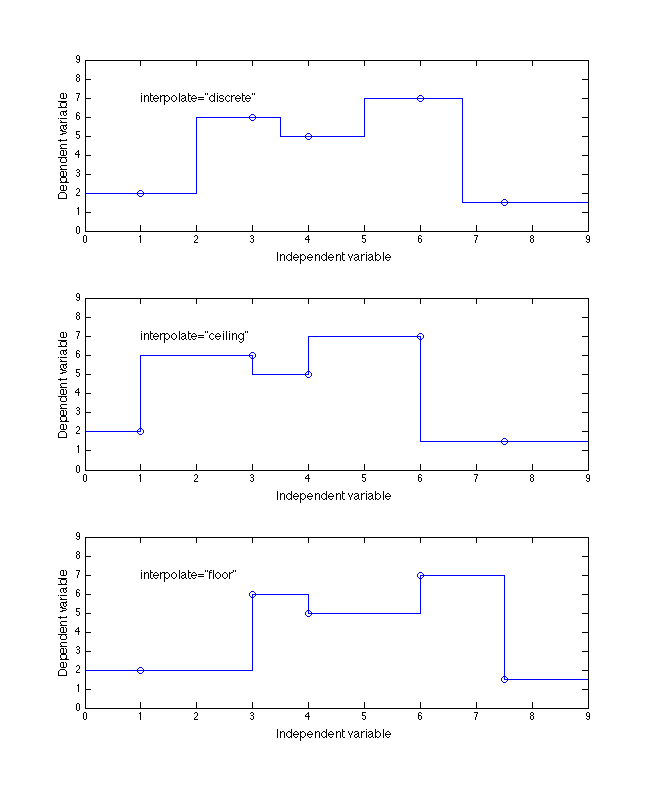
Figure 5. Examples of the three higher-order interpolation methods showing the effect of the
interpolate attribute of the
independentVarPts and
independentVarRef elements for a 1D
function table.